Пи (тоо)

Тоонуудай жагсаалта – Иррационал тоонууд ζ(3) – √2 – √3 – √5 – φ – α – e – π – δ
Хоёртын тоолол	11.00100100001111110110…
Аравтын тоолол	3.14159265358979323846…
16-тын тоолол	3.243F6A8885A308D31319…
Үргэлжэлһэн хубаагша	$3+\frac{1}{7+\frac{1}{15+\frac{1}{1+\frac{1}{292+\ddots }}}}$ Энэ үргэлжэлһэн хубаагшань дабтамжагүй гэдэгые анхаараарай.

Тойрогой диаметр 1 үедэ тэрэнэй утань π байна.

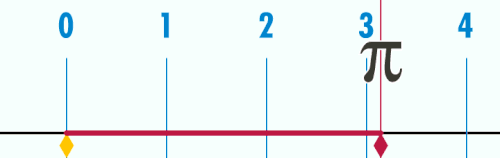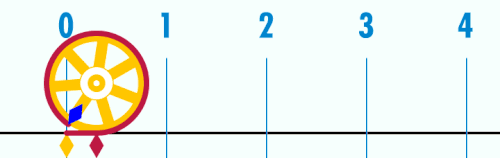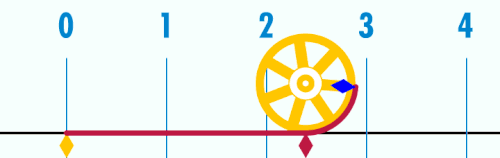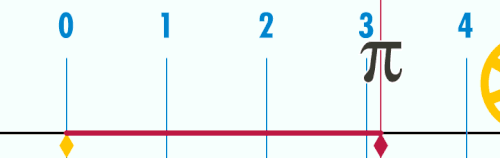
$\pi$ («пи» гэжэ дуудадаг) — ойролсоогоор 3.14159-тэй тэнсүү болон эгээн шухала математикын тогтомолнуудай нэгэ юм. Энэ тоонь Евклидэй геометрида алибаа тойрогой утые тэрэнэй диаметрта хубааһан харисаае элирхылдэг. Мүн тойрогой талмайе тэрэнэй радиусай квадратда хубааһан харисаагааршье элирхылжэ болодог. Пинь математика болон байгаалиин шэнжэлхэ ухаанай бусад олон томьёонуудта хэрэглэгдэдэг. Пи тоонь иррационал тоо болоод энэнь таһалалай арын оронууд 3.1415926535897932-нь дабтагдахагүйгээр түгэсхэлгүй үргэлжэлнэ гэһэн үгэ. Математикын түүхын туршада π-иие үндэр нарин нягтатайгаар тодорхойлжо, тэрэнэй шэнжэ шанарые шудалха гэһэн ехэхэн хүсэн шармайлтанууд зарсуулжа ерэһэн.

Грек үзэг π (ехэбшэлэн пи гэжэ бэшэдэг) периметр гэһэн Грек үгэһөө гаралтай. Магадгүй Уильям Джонс 1706 ондо энэ үзэгээр тэмдэглэһэн болон һүүлдэ хэдэн жэлэй дараа Леонард Эйлер энэниие түгээмэл болгоһон. "π"-иие грекээр пи гэжэ дуудадаг. Энэ тогтомолые мүн хааяа тойрогой тогтомол, Архимедай тогтомол (Архимедай тоотой андууржа болохогүй) гү, али Людольфын тоошье гэжэ дурдадаг.

Шэнжэ шанарнууд

Трансцендент ба иррационал шанарнууд

• $\pi$ — иррационал тоо юм
• $\pi$ — трансцендент тоо.
• $e^{\pi }$ баһал трансцендент тоо юм.
• $\pi$ хугасаанай сахаригай нэгэ элемент юм (тиимэһээ, $\pi$ тоосоологдохо болон арифметикын тоо юм).

Харилсаанууд

$\pi$ тооной олон томьёонууд байдаг:

• Франсуа Виет:

$\frac{2}{\pi }=\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{2+\sqrt{2}}}{2}\cdot \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}\cdot \dots$

• Валлисай томьёо:

$\frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdot \frac{8}{7}\cdot \frac{8}{9}\cdots =\frac{\pi }{2}$

• Лейбницай субарал:

$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots =\frac{\pi }{4}$

• Бусад субаралнууд:

$\begin{array}{cc}\pi & =\frac{1}{2}\sum _{k=0}^{\mathrm{\infty }}\frac{1}{16^k}(\frac{8}{8k+2}+\frac{4}{8k+3}+\frac{4}{8k+4}-\frac{1}{8k+7})\\ & =\frac{1}{4}\sum _{k=0}^{\mathrm{\infty }}\frac{1}{16^k}(\frac{8}{8k+1}+\frac{8}{8k+2}+\frac{4}{8k+3}-\frac{2}{8k+5}-\frac{2}{8k+6}-\frac{1}{8k+7})\\ & =\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{4^k}(\frac{2}{4k+1}+\frac{2}{4k+2}+\frac{1}{4k+3})\end{array}$

$\pi =2\sqrt{3}\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{3^k(2k+1)}$

• Олон тоо:

$\pi =8\sum _{k=1}^{\mathrm{\infty }}\sum _{m=1}^{\mathrm{\infty }}\frac{1}{(4m-2{)}^{2k}}=4\sum _{k=1}^{\mathrm{\infty }}\sum _{m=1}^{\mathrm{\infty }}\frac{m^2-k^2}{(m^2+k^2{)}^2}=\sqrt[4]{360\sum _{k=1}^{\mathrm{\infty }}\sum _{m=1}^k\frac{1}{m(k+1{)}^3}}$

• Хизаарнууд:

$\pi =\lim {\mathrm{\backslash limits}}_{m\to \mathrm{\infty }}\frac{(m!{)}^4{2}^{4m}}{{[(2m)!]}^{2}m}$

$\pi =\sqrt{\frac{6}{\lim {\mathrm{\backslash limits}}_{n\to \mathrm{\infty }}\prod _{\genfrac{}{}{0ex}{}{k=1}{p_k\in 𝐏}}^n(1-\frac{1}{p_k^2})}}\to$ здесь $p_k-$ простые числа

• Эйлерэй эжэл байдал:

$e^{i\pi }+1=0$

• Бусад тогтомолнуудтай харилсаа:

$\frac{\pi }{e}=2\prod _{k=1}^{\mathrm{\infty }}{\left(\frac{2k+1}{2k-1}\right)}^{2k-1}{\left(\frac{k}{k+1}\right)}^{2k}$

$\pi \cdot e=6\prod _{k=1}^{\mathrm{\infty }}{\left(\frac{2k+3}{2k+1}\right)}^{2k+1}{\left(\frac{k}{k+1}\right)}^{2k}$

• «Пуассонай интеграл» гү, али «Гауссай интеграл»

$\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}{e}^{-x^2}dx=\sqrt{\pi }$

• Интегралай синус:

$\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}\frac{\sin x}{x}dx=\pi$

• Дилогарифмаар элирхылэл:

$\pi =\sqrt{6{\ln }^{2}2+12{\mathrm{Li}}_2\left(\frac{1}{2}\right)}$

• Зохисгүй интегралаар элирхылэл:

$\underset{0}{\overset{+\mathrm{\infty }}{\int }}\frac{dx}{(x+1)\sqrt{x}}=\pi$